The integral of cos ( x) is sin ( x) + c, where c is a. Then du/dx = 2 we rearrange to get an expression for dx in terms of u.
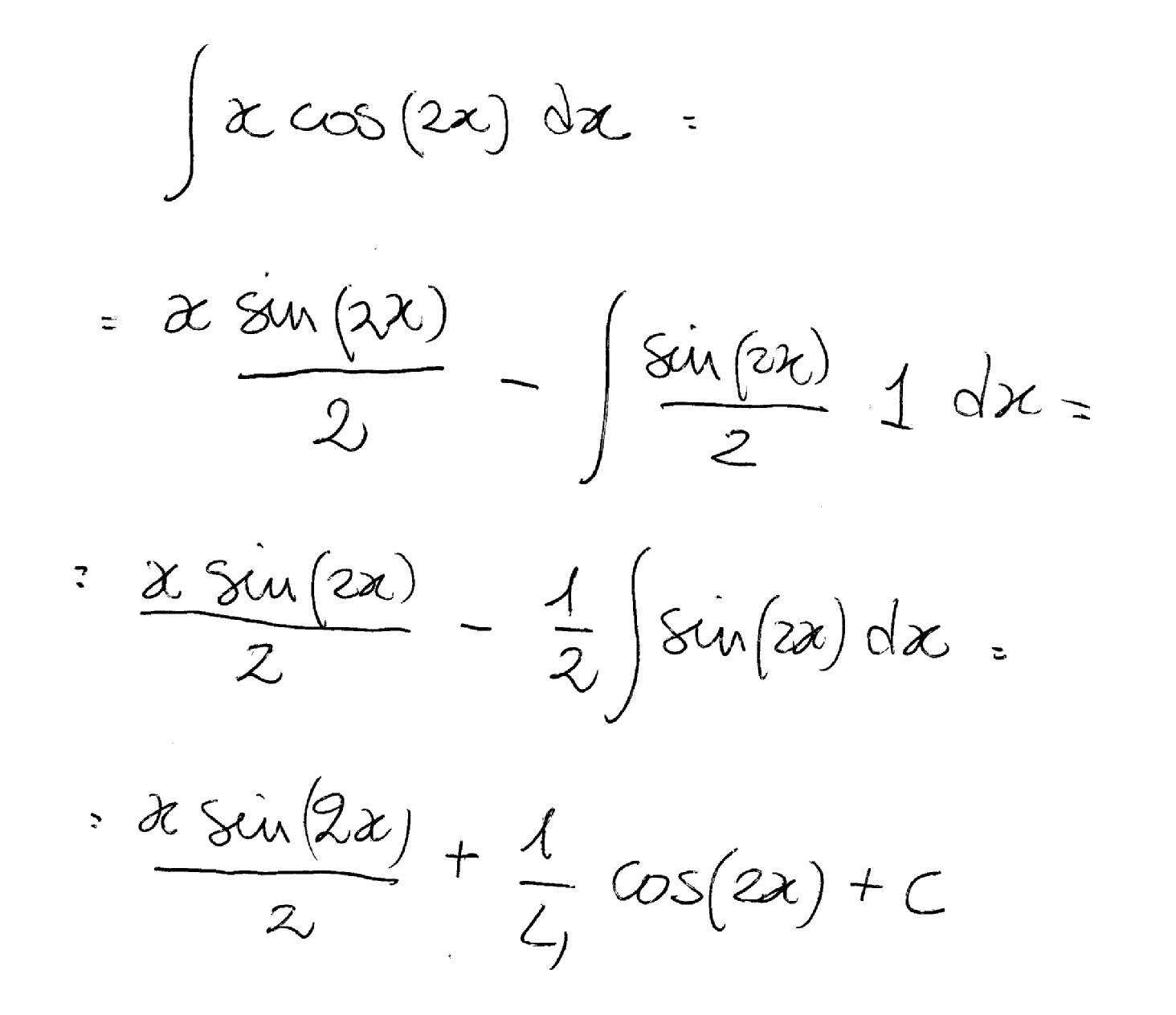
How Do You Integrate By Parts [Xcos2X]? | Socratic
Now we can rearrange this to give:
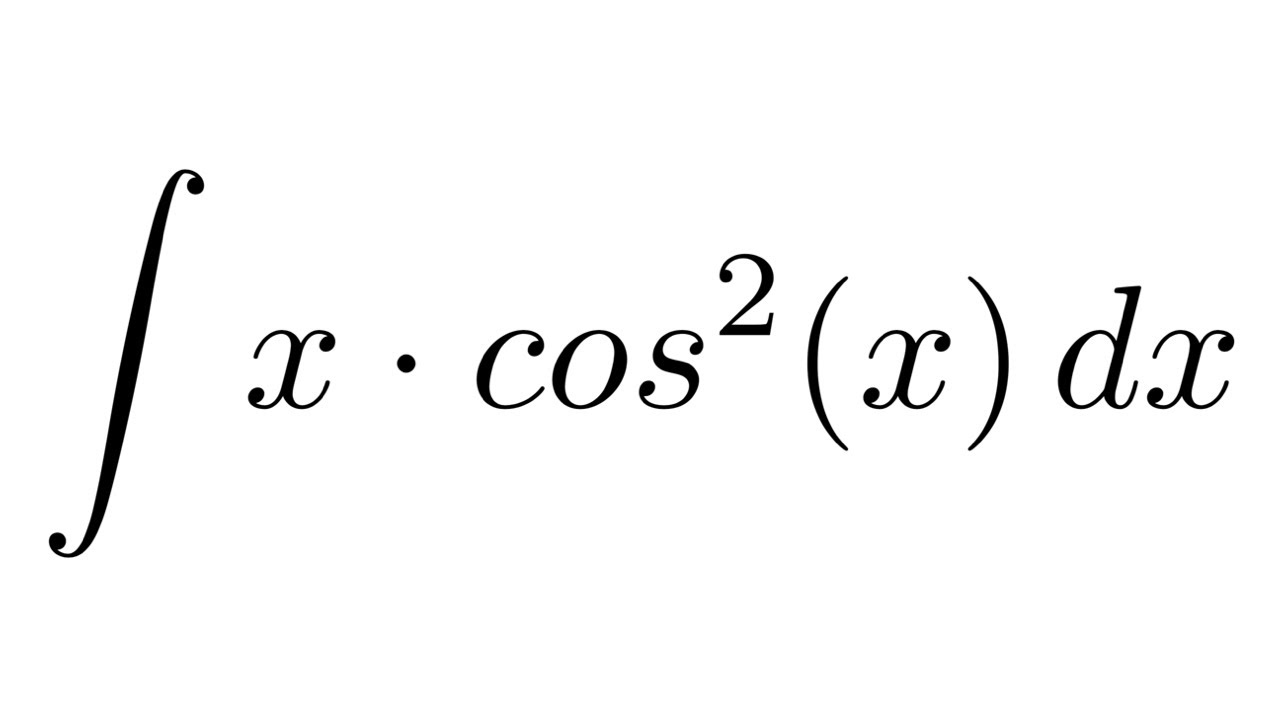
Integral of xcos2x. The easiest way to calculate this integral is to use a simple trick. Let u = 2x u = 2 x. Please subscribe my this channel also.
Int cosx dx = sin x +c int cos (x/2) dx = 2* sin (x/2) + c can be done by substitution x/2 = t → dx = 2dt etc. Class 7 science ncert solutions. Cos^2 (x) = (1+cos (2x))/2.
Integral of cos^5x show 10 more c4 integration by parts questio c4 trig. ∫ sin x dx, x ∈ [0, π/2] asked may 11, 2021 in definite integrals by kaina ( 30.5k points) definite integral To integrate cos2x, also written as ∫cos2x dx, and cos 2x, we usually use a u substitution to build a new integration in terms of u.
Class 10 science ncert solutions. Evaluate the following integral as a limit of sums: With the substitution t = ( 1 + i) x, this becomes.
What is the integration of x^2 cos2x dx? The function \sin (x)\cos (x) is one of the easiest functions to integrate. If we apply integration by parts to the rightmost expression again, we will get ∫\cos^2 (x)dx = ∫\cos^2 (x)dx, which is not very useful.
We recall the standard trig identity for cosecx, and square both sides. \[\int x\cos3x \, dx\] +. To integrate cosec^2x, also written as ∫cosec 2 x dx, cosec squared x, cosec^2 (x), and (cosec x)^2, we start by using standard trig identities to simplify the integral.
If there are two functions where one is differentiable (u) and one is integral (v),we use to solve the integration using in our case, and again,in (1) we see that we again have two functions.so, repeating the. Since 2 2 is constant with respect to x x, move 2 2 out of the integral. \frac du dx = \cos (x), or dx = du/\cos (x), which leads to another way to integrate the function is to use the formula so
The derivative of 2 x is 2. Evaluate the integral integral of 2cos (2x) with respect to x. Evaluate the integral integral of 2xcos (x) with respect to x.
First, we write \cos^2 (x) = \cos (x)\cos (x) and apply integration by parts: Integration c4 integration question c4 integration, help!!!! Let i = ∫xcos2xdx we use the rule of integration by parts, which is, ∫uvdx = u∫vdx − ∫[ du dx ∫vdx]dx we take, u = x,so du dx = 1;
1 ( 1 + i) 2 ∫ t e t d t = 1 ( 1 + i) 2 e t ( t − 1) = − 1 2 i e x ( cos x + i sin x) ( x − 1 + i x) (the antiderivative of t e t is an easy integration by parts). What is the integral of cos (x/2)? Hence, i = x 2 ⋅ sin2x − 1 2 ∫sin2xdx = x 2 ⋅ sin2x − 1 2 ( −cos2x 2) = 1 4 (2x ⋅ sin2x + cos2x) + c.
The second integral [ ∫ x/2 dx] is simple, integrating to x^2/4. Disregarding 1 2 e x, we have. For the first, trickier integral [∫ (xcos(2x))/2 dx], notice that this integral appears to be the multiple of two functions, so integration by parts is likely to come in handy.
∫ 2 cos(2x) dx ∫ 2 cos ( 2 x) d x. Integrating tan2x wjec c4 integration help. &v = cos2x,so,∫vdx = sin2x 2.
I also know the final answer does not contain an integral. As you can see, we now have a new integration in terms of. What i don't understand is how to get rid of the integral.
Then du = 2dx d u = 2 d x, so. Class 9 science ncert solutions. You get this by using integration by parts.
Set u = x/2 and dv/dx = cos(2x). Let i = and let differentiate on both sides now resubstituting we get i guess the sum is done johan yerramshetty All you need to do is to use a simple substitution u = \sin (x), i.e.
Since 2 2 is constant with respect to x x, move 2 2 out of the integral. Now compute the real part: So we have an equation that gives cos^2 (x) in a nicer form which we can easily integrate using the reverse chain rule.
Class 8 science ncert solutions. Integration question a level maths p3 help needed!! ∫ 2xcos (x) dx ∫ 2 x cos ( x) d x.
There are a few more facts that we need to know to be able to find this integral, and those are as follows: 2∫ xcos(x)dx 2 ∫ x cos ( x) d x. If the integral on the right in your example was + integral:
See answer (1) best answer. 2∫ cos(2x)dx 2 ∫ cos ( 2 x) d x.
Integration By Parts: Definite Integral Example - Youtube
Evaluate The Following Integrals Intx^2Cos2X Dx