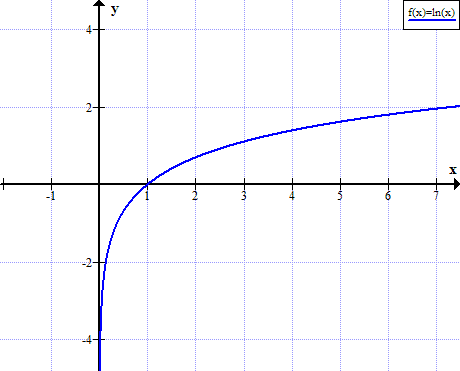
The limit of natural logarithm of infinity, when x approaches infinity is equal to infinity: The natural logarithm of zero is undefined:
Natural Logarithm Rules - Ln(X) Rules
Compute answers using wolfram's breakthrough technology & knowledgebase, relied on by millions of students & professionals.
What is ln infinity. Therefore, the value of log infinity to the base. Breed limited edition summer skins. Extended keyboard examples upload random.
Lim ln ( x) = ∞ x →∞ x approaches minus infinity the opposite case, the natural logarithm of minus infinity is undefined for real numbers, since the natural logarithm function is undefined for negative numbers: The limit near 0 of the natural logarithm of x, when x approaches zero, is minus infinity: Is ln of infinity infinity?
The natural logarithm of one is zero: The ln of 0 is infinity. The answer is +∞ you can prove it by reductio ad absurdum.
The hottest breeding event lunacia’s ever seen is live! You also know that ln(x2) − ln(x1) = ln( x2 x1) so if x2 > x1 the difference is positive, so ln(x) is always growing if lim x→∞ ln(x) = m ∈ r you have ln(x) < m ⇒ x < em, but x → ∞ so m can not be in r, and the limit must be +∞ So the top would be infinity as 0 is.
The natural log function is strictly increasing, therefore it is always growing albeit slowly. Base, a = 10 and 10 x = ∞. What is the ln of infinity?
The opposite case, the natural logarithm of minus infinity is undefined for real numbers, since the natural logarithm function is undefined for negative numbers: Logarithms were only defined for positive numbers. You can think of the integral as a series, sum(1/x) from 1 to infinity which is 1/1+1/2+1/3+1/4+1/5… does 1 lnn converge?
Origin is now available to play via mavis hub! Natural logarithm rules and properties what is the ln of zero? The log function of infinity to the base 10 is denoted as “log 10 ∞” or “log ∞”.
21 what is the value of ln (0) and nature of natural logarithm at. In terms of the limit we might say that ln (x) goes to negative infinity as x goes to 0. Since abs(1/ln(n)) is larger than 1/n as n gets larger the convergence condition is not satisfied, and since for n larger than 1, ln(n) is positive number the sum gets larger as n gets larger the sum does not convergence.
According to the definition of the logarithmic function, it is observed that. You know that if x > 1ln(x) > 0 so the limit must be positive. No, the logarithm of 0 (to any base) does not exist.

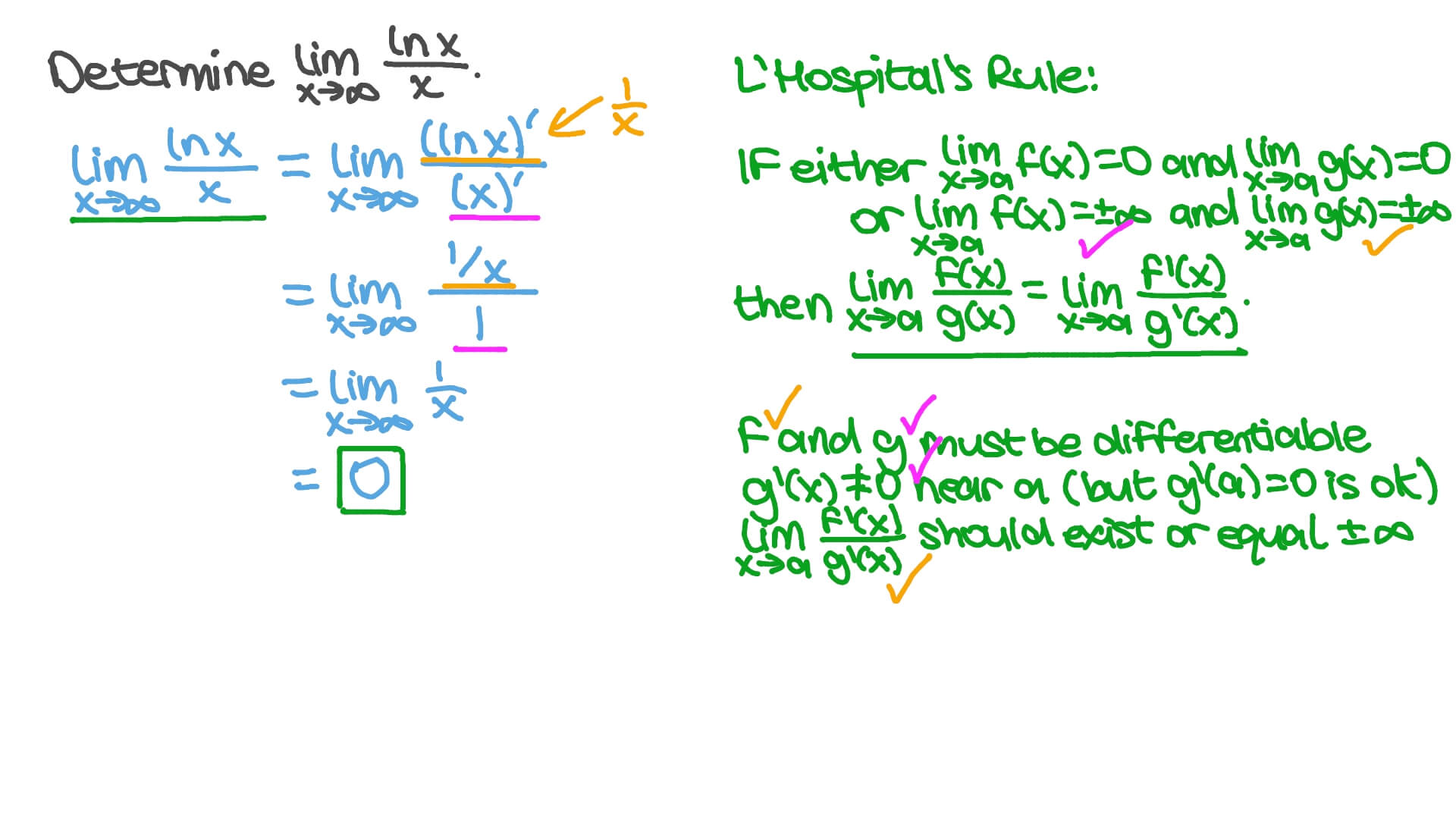
Calculus - Ln(Infinity/Infinity) - Mathematics Stack Exchange
