If the second derivative is zero at the critical points, then the test fails. The value of the function at a maximum point is called the maximum value of the function,.

Learn How To Find The Absolute Max, Min And Relative Max Min Of A Graph - Youtube
To allude to the example.
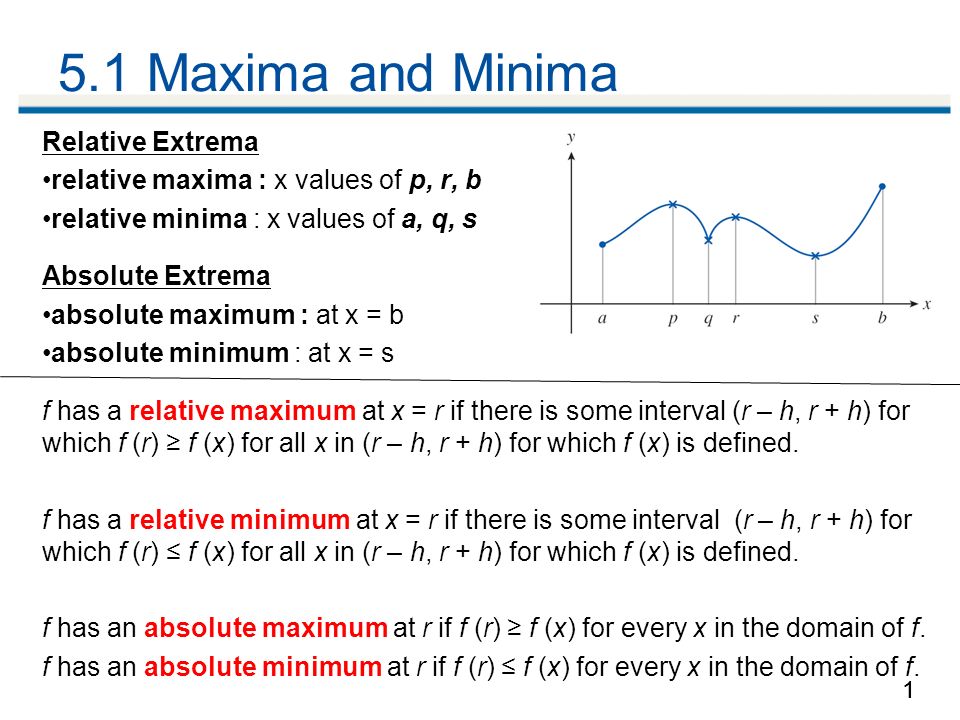
Absolute vs relative maxima. F' (x) = 0, or 6x 2. Relative return example one way to look at absolute return versus relative return is in the context of a market cycle, such as bull versus bear. (i) in the given interval in f, find all the critical points.
A relative minimum is a location on a curve. These may also be referred to as relative maxima and minima instead of local maxima and minima. So, relative extrema will refer to the relative minimums and maximums while absolute extrema refer to the absolute minimums and maximums.
Now, let’s talk a little bit. These are located by tracking where the function changes from increasing to decreasing (relative maximum) or. Relative is always in proportion to a whole.
If a substance’s relative density is less than one then it is less dense than the reference and will float in water. F” > 0, if it is a minima. 🔗 3.1.2 identifying relative extrema 🔗 a relative maximum is a location on a curve where all points near it are lower.
Absolute maxima is the greatest value of the continuous function for given closed interval and absolute minima is the smallest value of continuous function on given closed interval. Frequently, the interval given is the. 12th pass out (maths physics and chemistry.) 5 y local minima and maxima is the minimum and maximum of a function in a particular region while absolute maxima and minima is the.
F” < 0, if it is a maxima. Consider the function (a) without graphing, show that f has an absolute minimum on the interval (0, 2). , the second derivative test fails.
Sal gives multiple examples where he identifies relative maximum points, relative minimum points, absolute maximum points, and absolute minimum points.practi. The derivative is which is defined everywhere, so the critical. Absolute changes on small numbers can look small even if their relative changes are large.
Analyzing a function with its derivative. Here we equalize this derivative to zero, to find the limiting points. Similarly, the function has a global (or absolute) minimum point at x∗, if f(x∗) ≤ f(x) for all x in x.
Similarly, an absolute minimum point is a point where the function obtains its least possible. Absolute changes work the other way: Relative extrema are simply the bumps and dips on a function’s graph.
An absolute extremum (or global extremum) of a function in a given interval is the point at which a maximum or minimum value of the function is obtained. An absolute maximum point is a point where the function obtains its greatest possible value. (ii) calculate the value of the functions at all the.
Because the absolute highest point on the curve will often be your absolute maximum, and the absolute lowest point on your curve will be your absolute minimum. And also, global maxima and minima are the same as absolute maxima. Thus we go back to the first derivative test.
• absolute evaluation or analysis means an individual, product, or idea is not compared with any other entity, and its performance is judged free from other criteria. Let us take the first derivate of this function, to find the relative maxima of the function.
Relative Vs Absolute Extrema – Math Faq
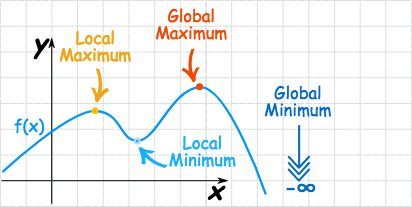
Extrema: Maxima & Minima. Extrema Are One Type Of Critical… | By Solomon Xie | Calculus Basics | Medium