So n equals one, two, three, all the way on, and on, and on. Thanks to all of you who support me on patreon.

Comparison Test. You Can Understand Comparison Test… | By Solomon Xie | Calculus Basics | Medium
Let an = e1 n n and bn = 1 n, noting that an > bn > 0 for all integers n > 0.
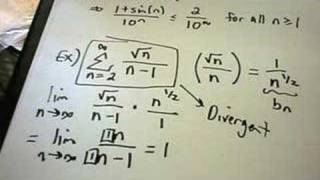
When to use direct comparison vs limit comparison. I’ll provide the mathematical statement, but also how you should think about the. Σ1/(n^2+1) so here i can simply. Since the limit you calculated is 1,.
Use the limit comparison test to determine if the series converge or diverge. The limit comparison test is a good test to try when a basic comparison does not work (as in example 3 on the previous slide). For two series, where l is finite and positive, either both series converge or both diverge.
For problems 11 { 22, apply the comparison test, limit comparison test, ratio test, or root test to determine if the series converges. Start date nov 16, 2006; Thanks to all of you who support me on patreon.
Once again, this is true for all the ns that we care about. Because this denominator is always going to be greater by one if you're denominator is greater, the overall expression is going to be less, and because of that, because each of these terms. \sum_ n=3^ \infty\frac n^2+n^3 \sqrt {n^8+n^4} ∑n=3∞ n8+n4 n2+n3 \sum_ n=1^ \infty\frac 1 {n^2.
The direct comparison test often compares a series to either or. If it is less than a convergent series, it converges. I'm not really sure when each of these should be done.
Now compute lim n→∞ an bn. 1 comparison test requires qn ⩽ bn,∀n and if ∑bn is convergent then ∑qn is also convergent. So the comparison test tells us that.
If c is positive and finite then either both diverge or both converge. The principal tests for convergenceor divergence are the. The comparison test is easier to implement, but it has a strict requirement that the limit.
1 the statement of the limit comparison test in order to use limit comparison, we have to know the statement. The idea of this test is that if the limit of a ratio of sequences. If it converges we can use numerical methods to approximate its value.
If ∑bn is divergent then ∑qn is also divergent. This is a good test to use when you can’t use the direct. In fact, i don't really understand the reason that we use the limit comparison test.
If the integral diverges, we are done. Hi all, i’m trying to study for a calc 2 exam and am going over series. The limit comparison test, by contrast, says that if the limit you calculated is some positive real number, then both integrals converge or both diverge.
If it is larger than a divergent series, it diverges. I’m stuck on limit and direct comparison, and more specifically which i. Less than or equal to b sub n.
Joined nov 16, 2006 messages 2. We arehoping it is a positive number and not ∞, which will. Remember for limit comparison, we take the expressions in the two series we are comparing and form the ratio.
State which test you are using, and if you use a.

Using The Direct Comparison Test To Determine If A Series Converges - Dummies
