Practice your math skills and learn step by step with our math solver. This video demonstrates how you can use the magic hexagon to generate commonly used trig identities.
How To Prove Quotient And Reciprocal Identities | Studypug
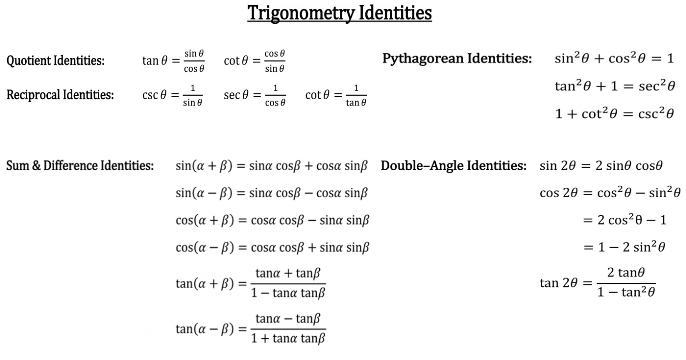
Sin2 a + cos2 a = 1 1+tan2 a = sec2 a cosec2 a = 1 + cot2 a ratio trigonometric identities the trigonometric ratio identities are:

Quotient identiies trig. Among other uses, they can be helpful for simplifying trigonometric expressions and equations. Slide 1 trig identities slide 2 reciprocal identities or pythagorean identities or quotient identities slide 3 tips for proving trigonometric identities: The organic chemistry tutor 4.63m subscribers this trigonometry video tutorial explains how to evaluate tangent and cotangent trigonometric functions using the quotient identities of tan and cot.
Cotangent, if you're unfamiliar with. Trigonometric identities are equations that are used to describe the many relationships that exist between the trigonometric functions. Sec ( x) 2 + csc ( x) 2 = 1 sin ( x) 2 · cos ( x) 2 go!
The equation tan θ = sin θ cos θ is therefore an identity that we can use to find the value of the tangent function, given the value of the sine and cosine. They are called the quotient trigonometric identities and simply called as quotient identities. The basic trig identities or fundamental trigonometric identities are actually those trigonometric functions which are true each time for variables.so, these trig identities portray certain functions of at least one angle (it could be more angles).
Start studying trig identities quiz. The sine, cosine, tangent and cotangent functions are written as sin θ, cos θ, tan θ and cot θ respectively. Let's take a look at some problems involving quotient identities.
If all else fails, use the reciprocal identities and quotient identities. Check out all of our online calculators here! The following shows some of the identities you may encounter in your study of trigonometry.
Tan θ = sin θ/cos θ cot θ = cos θ/sin θ There are two quotient identities that can be used in right triangle trigonometry. In trigonometry, trigonometric identities are equalities that involve trigonometric functions and are true for every value of the occurring variables for which both sides of the equality are defined.
There are two quotient identities that can be used in right triangle trigonometry. It is identified with a unit circle where the connection between the lines and angles in a cartesian plane. This version of the magic hexagon, as well as many othe.
Sin^2 θ + cos^2 θ = 1 tan^2 θ + 1= sec^2. However, here are some clues to narrow down which identities you should try. ( ) / ÷ 2 √ √ ∞ e π
In here, one is the quotient we get after division operation between the other two. Geometrically, these are identities involving certain functions of one or more angles. To play this quiz, please finish editing it.
Find the value of tan θ? When the angle of a right triangle is represented by theta. If cos θ = 5 13 and sin θ = 12 13, what is the value of tan θ?
View trig+identities.odt from math 095 at college of southern nevada. A quotient identity defines the relations for tangent and cotangent in terms of sine and cosine. In trigonometry, quotient identities refer to trig identities that are divided by each other.
For instance, tan θ = sin θ /cos θ and cot θ = cos θ / sin θ. Remember that the difference between an equation and an identity is that an identity will be true for all values. Substitute the appropriate values into the identity and simplify:
Tan θ = 12 5 Pythagorean identities tan +1>sec cot +1>csc. Learn vocabulary, terms, and more with flashcards, games, and other study tools.
The two possible cases are used as formulas in trigonometry. The following is a list of useful trigonometric identities: There are two quotient identities that are crucial for solving problems dealing with trigs, those being for tangent and cotangent.
Download as pdf file [trigonometry] [differential equations] Trigonometric identities reciprocal identities quotient identities pythagorean identities cofunction identities opposite angle A quotient identity defines the relations for tangent and cotangent in terms of sine and cosine.

Reciprocal Identities - Formulas, Proof, Examples

What Are The Quotient Identities For A Trigonometric Functions?