Log e (72) ln(72) 4.276666: The natural logarithm of a number x is defined as the base e logarithm of x:
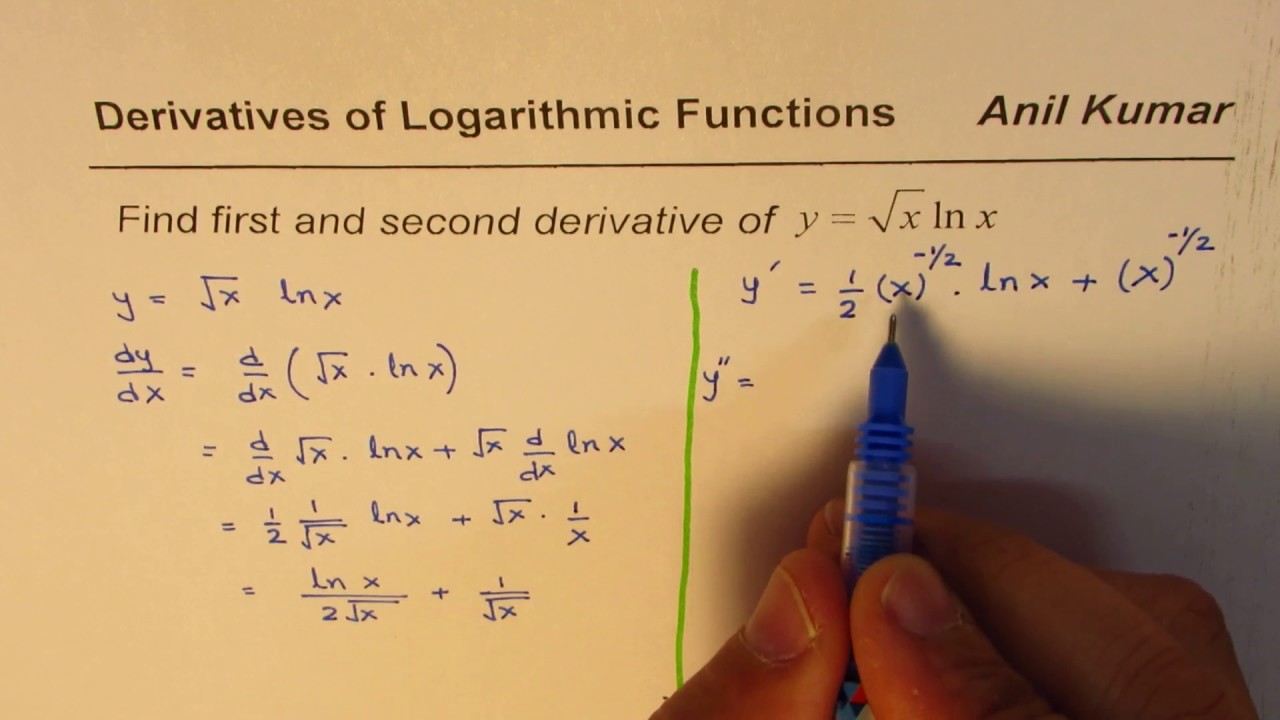
First And Second Derivative Of Sqrt X Ln X - Youtube
Ln(x) is asking e to the power of what is x in this case, e to the power of 2 is e2 thus, ln(e2) = 2 another way is using the property of logarithms that says ln(ab) = b ⋅ ln(a) in this case, a = e and b = 2 thus, ln(e2) = 2 ⋅ ln(e) = 2 ⋅ 1 = 2 answer link
Ln square root e equals. Log e (71) ln(71) 4.26268: Natural logarithm of negative number. Square roots is a specialized form of our common roots calculator.
Ln(x) = log e (x) so the natural logarithm of e is the base e logarithm of e: 💬 👋 we’re always here. Ln(e) = log e (e) = 1.
Using the calculator, \(\sqrt[11]e\) = 1.0951694398746643 Lmt and ellen is equal to one for this candidate and through seven in total seven, which is equal to seven. Log e (66) ln(66) 4.189655:
The result can be shown in multiple forms. I will assume you mean the 11th root of e. Log in ag ankit g.
The natural logarithm can be defined for any positive real number a as the area under the curve y = 1/x from 1 to a [3] (with the area being negative when 0 < a < 1 ). Log e (68) ln(68) 4.219508: The natural logarithm of e itself, ln e, is 1, because e1 = e, while the natural logarithm of 1 is 0, since e0 = 1.
Lim ln(x) = ∞ x→∞. Log e (73) ln(73) 4.290459: Log e (67) ln(67) 4.204693:
So the natural logarithm of e is equal to one. Well, we know how to take the derivative of u of x and v of x, u prime of x here, is going to be equal to, well remember, square root of x is just the same thing as x to 1/2 power, so we can use the power rule, bring the 1/2 out from so it becomes 1/2 x to the, and then take off one out of that exponent, so that's 1/2 minus one is negative 1/2. Graph two equations to determine every real number whose square equals its cube.
So you would make 1ln (x)^0.5. Since exponentiating e and ln's are inverses, for all expressions for p.) 2. Log e (76) ln(76) 4.330733:
Join our discord to connect with other students 24/7, any time, night or day. Log e (69) ln(69) 4.234107: I'm assuming the problem is if so, please use parentheses on multiple term exponents:
Log e (77) ln(77) 4.343805: Log e (74) ln(74) 4.304065: Ln(e) = log e (e) ln(e) is the number we should raise e to get e.
Note that any positive real number has two square roots, one positive and one negative. Write the given expression as a single logarithm. We now have the desired form.
Where u=ln (x)^0.5 (dv/dx) = 1 diffrentiate u to get (du/dx) = no idea what this equals actually. E ≈ 2.71828183 ln as inverse function of exponential function the natural logarithm function ln (x) is the inverse function of the exponential function e x. Evaluate e^ ( natural log of square root of 5) eln(√5) e ln ( 5) exponentiation and log are inverse functions.
Write the given expression as a single logarithm. Log e (75) ln(75) 4.317488: The e constant or euler's number is:
No sure how to differentiate (ln (x))^0.5. Since represents the exponent for e which results in and since it is the exponent for e in this expression, (alternate explanation: The opposite case, the natural logarithm of minus infinity is undefined for real numbers, since the natural logarithm function is undefined for negative numbers:
Write the given expression as a single logarithm. Log e (70) ln(70) 4.248495:

Natural Log Ln(1/√E) With A Square Root Evaluate By Definition Fwk 07-0302 - Youtube
